False Precision
The use of p-values to indicate the probability of something occurring by chance may be misleading.
Key Concepts addressed:- 2-17 Don’t confuse “statistical significance” with “importance”
- 2-16 Confidence intervals should be reported
Details
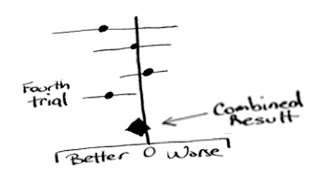
Precise numbers and claims – as though there is no margin for error – are all around us. When someone tells you that 54.3% of people with some disease will have a particular outcome, they’re basically predicting the future of all groups of people based on what happened to another group of people in the past. Well, what are the chances of that, eh?
If our fortune teller was quoting the mean of a study here, it could be written like this: 67.5% (95% CI: 62%-73%). The CI stands for “confidence interval” and measures the range of the data. It’s showing us that 95 times out of 100, similar data sets to which the statistical test was applied would show a mean somewhere between 62% and 73%.
The chances of the result always being precisely 67.5% can be pretty slim or very high, depending on lots of things. If there is a lot of data, the confidence interval will be narrow: the best case scenario and the worst case scenario will be close together (say, 66% to 69%).
Cartoons are available for use, with credit to Hilda Bastian.